Dopo aver accennato al classico teorema di Sklansky, Flavio Ferrari Zumbini, pro del team Glaming, analizza con Rudy Gaddo l'enunciato noto come teorema di Beluga. Spiegazione del teorema fondamentale del poker Immaginate che, la prossima volta che vi siederete ad un tavolo, le carte dei vostri avversari fossero tutte scoperte. In questo caso, conosceremo sempre la forza della mano dei nostri avversari, e sapremo sempre come comportarci. The fundamental theorem of poker is a principle first articulated by David Sklansky that he believes expresses the essential nature of poker as a game of decision-making in the face of incomplete information.

1. Teorema Fondamentale Del Poker
2. Teorema Del Poker Game

Con l'espressione teorema fondamentale del poker si indica questo enunciato di David Sklansky:

Sebbene sia indicato nel linguaggio comune come teorema, esso non può essere definito tale. In ogni caso questo enunciato si basa su dei solidi principi matematici: nel poker ogni decisione è basata sul concetto di valore atteso. Nel poker generalmente i giocatori possono puntare o rilanciare, accettare una puntata o non piazzarne alcuna e hanno sempre la possibilità di ritirarsi dalla mano. La scelta giusta e la quantità di gettoni da investire è quella che più aumenta il valore atteso.

Contenuto[modifica modifica wikitesto]

L'enunciato afferma semplicemente che conoscendo le carte del proprio avversario si ha sempre la certezza della scelta giusta da fare per vincere nel lungo termine. Ne risulta quindi che una capacità fondamentale del giocatore di poker è la 'lettura dell'avversario' (read), ossia la capacità di individuare il 'range' dell'avversario, ossia di capire con quale ventaglio di carte sta giocando o addirittura capire con precisione quali siano. Di contro è altrettanto importante riuscire a impedire al giocatore avversario di capire il proprio range e in generale il proprio gioco. Riassumendo, l'enunciato suggerisce che per vincere bisogna trarre in inganno l'avversario facendogli fare degli errori.

Collusione implicita[modifica modifica wikitesto]

Il teorema fondamentale, però, manca di efficacia quando si sta parlando di piatti multi-way, ossia quando non si gioca contro un solo avversario. Questo a causa della cosiddetta collusione implicita, come spiega il teorema di Morton.

Bibliografia[modifica modifica wikitesto]

• David Sklansky, The Theory of Poker. Las Vegas, Two Plus Two Publishing, 1999. ISBN 9781880685006

Voci correlate[modifica modifica wikitesto]

The fundamental theorem of poker is a principle first articulated by David Sklansky that he believes expresses the essential nature of poker as a game of decision-making in the face of incomplete information.

Every time you play a hand differently from the way you would have played it if you could see all your opponents' cards, they gain; and every time you play your hand the same way you would have played it if you could see all their cards, they lose. Conversely, every time opponents play their hands differently from the way they would have if they could see all your cards, you gain; and every time they play their hands the same way they would have played if they could see all your cards, you lose.

The fundamental theorem is stated in common language, but its formulation is based on mathematical reasoning. Each decision that is made in poker can be analyzed in terms of the expected value of the payoff of a decision. The correct decision to make in a given situation is the decision that has the largest expected value. If a player could see all of their opponents' cards, they would always be able to calculate the correct decision with mathematical certainty, and the less they deviate from these correct decisions, the better their expected long-term results. This is certainly true heads-up, but Morton's theorem, in which an opponent's correct decision can benefit a player, may apply in multi-way pots.

An example[edit]

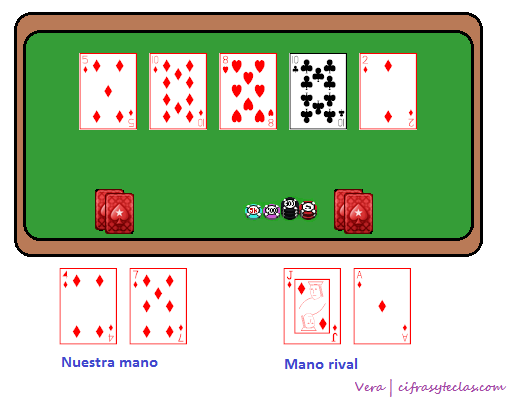
Suppose Bob is playing limit Texas hold 'em and is dealt 9♣ 9♠under the gun before the flop. He calls, and everyone else folds to Carol in the big blind who checks. The flop comes A♣ K♦ 10♦, and Carol bets.

Bob now has a decision to make based upon incomplete information. In this particular circumstance, the correct decision is almost certainly to fold. There are too many turn and river cards that could kill his hand. Even if Carol does not have an A or a K, there are 3 cards to a straight and 2 cards to a flush on the flop, and she could easily be on a straight or flush draw. Bob is essentially drawing to 2 outs (another 9), and even if he catches one of these outs, his set may not hold up.

However, suppose Bob knew (with 100% certainty) that Carol held 8♦ 7♦. In this case, it would be correct to raise. Even though Carol would still be getting the correct pot odds to call, the best decision for Bob is to raise. Therefore, by folding (or even calling), Bob has played his hand differently from the way he would have played it if he could see his opponent's cards, and so by the fundamental theorem of poker, his opponent has gained. Bob has made a 'mistake', in the sense that he has played differently from the way he would have played if he knew Carol held 8♦ 7♦, even though this 'mistake' is almost certainly the best decision given the incomplete information available to him.

This example also illustrates that one of the most important goals in poker is to induce the opponents to make mistakes. In this particular hand, Carol has practiced deception by employing a semi-bluff — she has bet a hand, hoping Bob will fold, but she still has outs even if he calls or raises. Carol has induced Bob to make a mistake.

Multi-way pots and implicit collusion[edit]

The Fundamental Theorem of Poker applies to all heads-up decisions, but it does not apply to all multi-way decisions. This is because each opponent of a player can make an incorrect decision, but the 'collective decision' of all the opponents works against the player.

This type of situation occurs mostly in games with multi-way pots, when a player has a strong hand, but several opponents are chasing with draws or other weaker hands. Also, a good example is a player with a deep stack making a play that favors a short-stacked opponent because he can extract more expected value from the other deep-stacked opponents. Such a situation is sometimes referred to as implicit collusion.

The fundamental theorem of poker is simply expressed and appears axiomatic, yet its proper application to the countless varieties of circumstances that a poker player may face requires a great deal of knowledge, skill, and experience.

Teorema Fondamentale Del Poker

See also[edit]

Teorema Del Poker Game